So you wake up one morning and your space is curved.
Your first thought is: how curved? is my space slightly curved? or is it seriously curved?
Happily, your pet two-dimensional crab has an easy way to find out.
Here’s how to measure the curvature of your space.
—
Remember when our two-dimensional crab moved an equal distance in every possible direction and measured how much space it covered?
It found that when it moved 1 crab length in every possible direction, it covered 3.14 crabs’ worth of space:
If you recall, you can count the number of crabs that fit into the space it covers. There’s a crab in the middle, with half a crab above it, half a crab below it, two more half-crabs either side, plus some small bits of a crab. That’s a total of three and a bit crabs’ worth of space. 3.14 crabs’ worth, to be precise.
When the crab moved 2 crab lengths in every possible direction, it covered 12.57 crabs’ worth of space:
When it moved 3 crab lengths, it covered 28.27 crabs’ worth of space:
When it moved 4 crab lengths, it covered 50.27 crabs’ worth of space:
And when the crab moved 5 crab lengths in every possible direction, it covered 78.54 crabs’ worth of space:
For a mathematically-minded crab, it’s easy to find the formula that fits this progression. Whenever the crab moves r crab lengths in every possible direction, it covers π r2 crabs’ worth of space:
V = π r2
It’s even easier for us, with our God’s-eye view of the crab’s two-dimensional space, to find the formula. Every time the crab moves an equal distance in every possible direction, it carves out a circle of space. And the area of a circle is π r2.
The point is that even without our God’s-eye perspective, the crab can find the formula V = π r2, and from that 2 in the formula, determine that its universe is two-dimensional:
V = π r2
But everything I’ve said so far assumes a flat universe.
What if the crab’s universe is curved?
Ever decreasing circles
Let’s imagine that our two-dimensional crab is in a spherical two-dimensional space:

Our crab is feeling pretty confident these days that it knows everything there is to know about itself and its universe.
It knows that it’s a two-dimensional crab in a two-dimensional space.
And it knows how to prove that it’s a two-dimensional crab in a two-dimensional space.
For old times’ sake, it decides to test the two-dimensionality of its space once again.
So it goes for a walk.
It moves r = 1 crab length in every possible direction, knowing that it’ll cover V = π r2 = 3.14 crabs’ worth of space. And sure enough, it finds that it has covered... 3.13 crabs’ worth of space:

Well, that’s near enough. Even a weirdly precise crab can’t get too worried about an imprecision of less than half a percent.
Next, it moves r = 2 crab lengths in every possible direction, imagining that it’ll cover V = π r2 = 12.57 crabs’ worth of space. And it finds that it has covered... 12.38 crabs’ worth of space:
Now that is a little worrying. That’s a one-and-a-half percent discrepancy. Something’s not right here.
The crab presses on, moving r = 3 crab lengths in every possible direction. Instead of covering V = π r2 = 28.27 crabs’ worth of space, it finds that it has covered 27.36 crabs’ worth of space, fully three percent less than expected:
The further the crab moves, the greater the discrepancy. Moving r = 4 crab lengths, the crab covers 47.39 crabs’ worth of space, over five percent less than the formula V = π r2 predicts:
Moving r = 5 crab lengths, it covers 71.62 crabs’ worth of space, over eight percent less than predicted:
And then things start to go seriously awry. Moving r = 6 crab lengths, the crab covers 98.98 crabs’ worth of space, instead of 113.10:
Moving r = 7 crab lengths, it covers 128.27 crabs’ worth of space, instead of 153.94:
Moving r = 8 crab lengths, it covers 158.21 crabs’ worth of space, instead of 201.06:
By the time the crab is moving r = 9 crab lengths in every possible direction, it’s covering over 25% less space than the formula V = π r2 predicts, 187.50 crabs’ worth instead of 254.47:
The crab is perplexed.
What’s going on?
Mathematically minded
Our curious crab begins to wonder whether its universe is truly two-dimensional after all.
Since it’s a mathematically minded crab, it draws a graph.
It plots the amount of space it actually covered, V, against the distance it moved in every possible direction, r.
That’s the red line.
On the same axes, it plots the amount of space it anticipated covering, V = π r2.
That’s the blue line.
The two lines aren’t so far apart, at least at first:
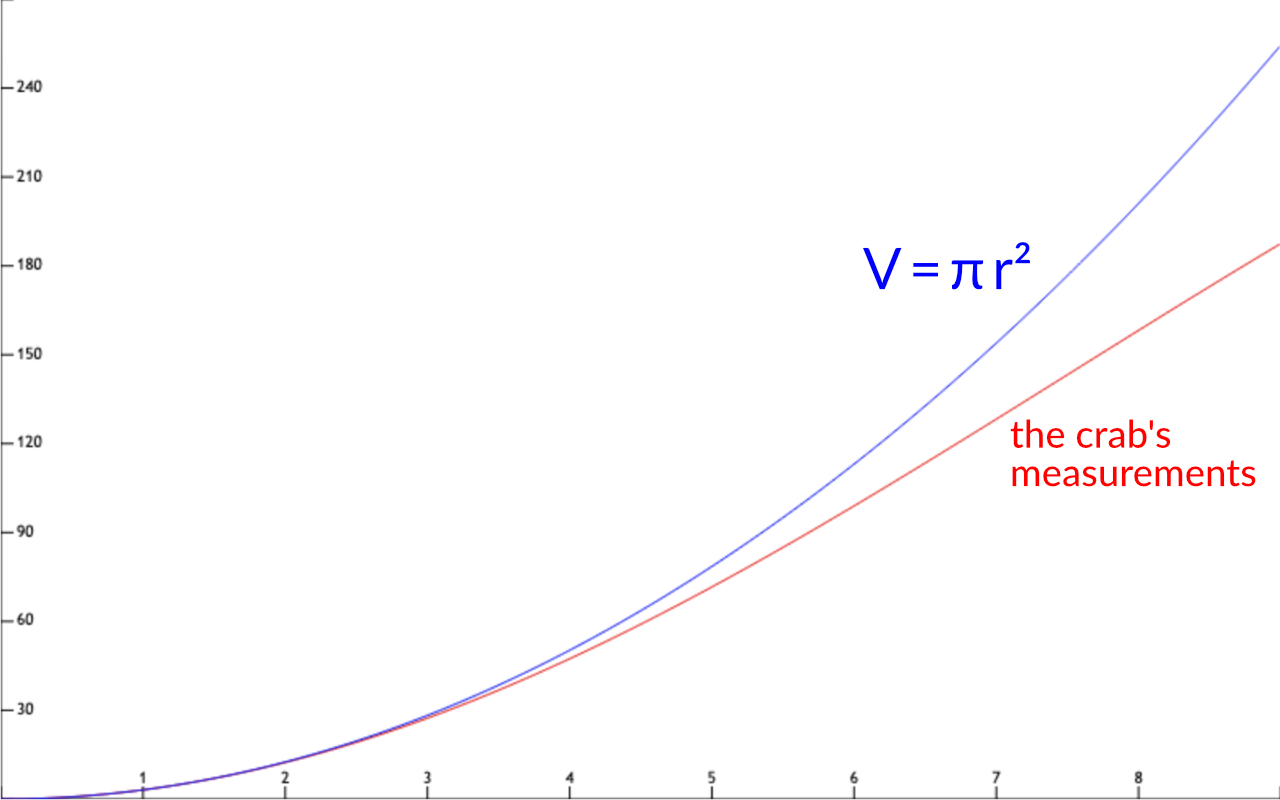
So maybe the crab’s space is approximately two-dimensional... whatever that means!
The crab also plots the amount of space it would anticipate covering if its space were one-dimensional, V = 2 r, and the amount of space it would anticipate covering if its space were three-dimensional, V = 4/3 π r3.
These lines really are a long way from the crab’s measurements:
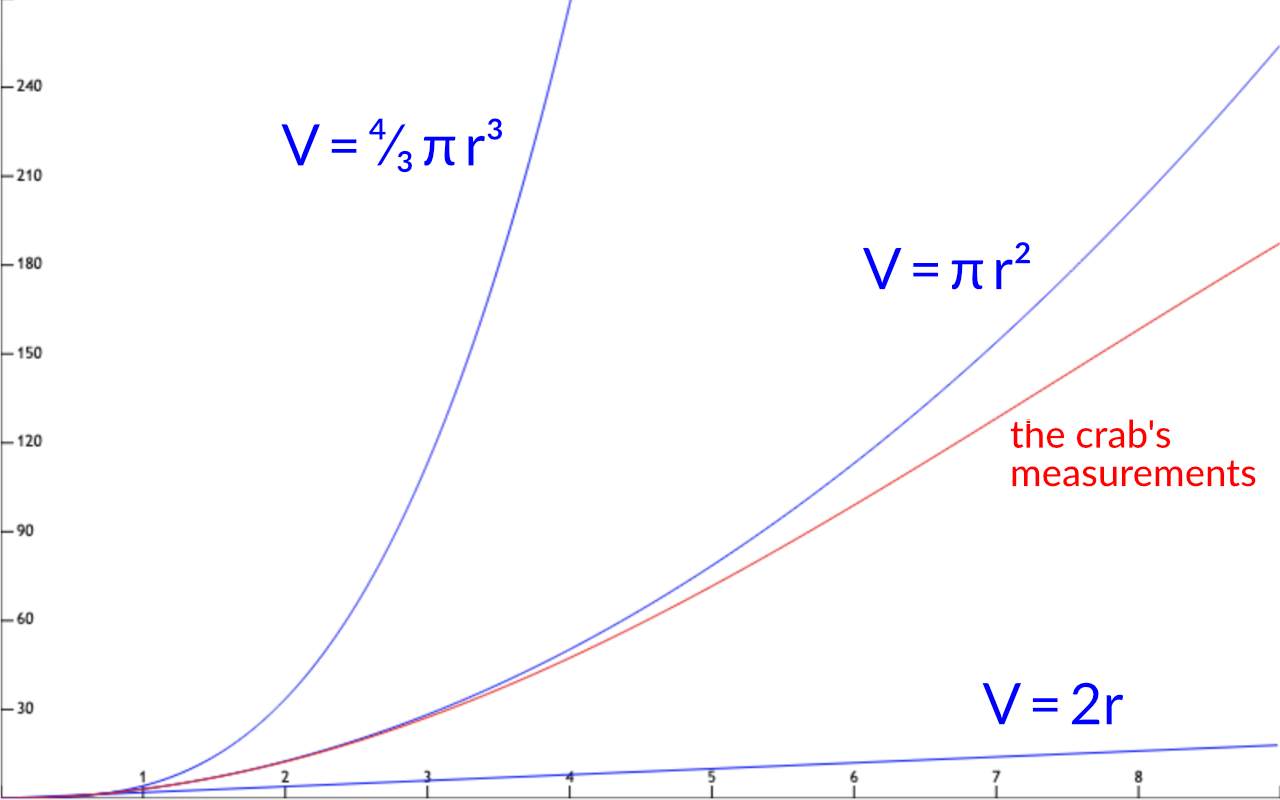
So the crab’s space is definitely closer to two-dimensional than one-dimensional or three-dimensional.
Then the crab has an idea. Maybe its space has a fractional number of dimensions? Since the red line for its measurements is somewhere between the blue line for a one-dimensional universe and the blue line for a two-dimensional universe, maybe its universe has somewhere between one and two dimensions?
But that doesn’t work, either. The best fit the crab can come up with is a 1.9-dimensional universe. The line for this universe, plotted in green, is certainly closer to the line for the crab’s measurements, plotted in red. Still it’s not an exact match. It starts too low and ends too high:
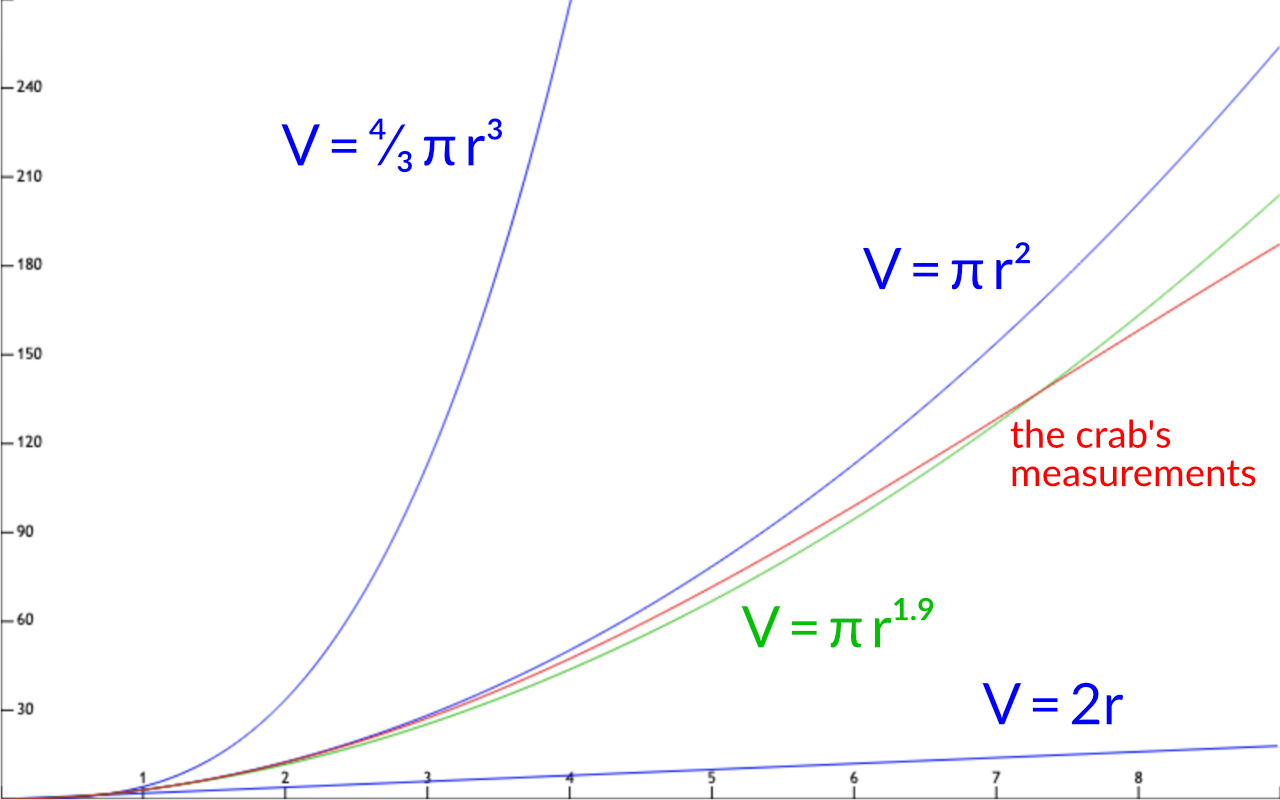
No matter what number of dimensions the crab tries, there’s no way to explain how the amount of space it actually covered is related to the distance it moved.
Power move
Our crab is nothing if not persistent.
If the formula that fits the measurements isn’t r2 or r1 or r3 or even r1.9, then some combination of powers r1, r2, r3, r4, etc. must work.
So the crab does a polynomial analysis and finds that a formula with just two terms – π r2 with a small r4 correction – fits its measurements much better:
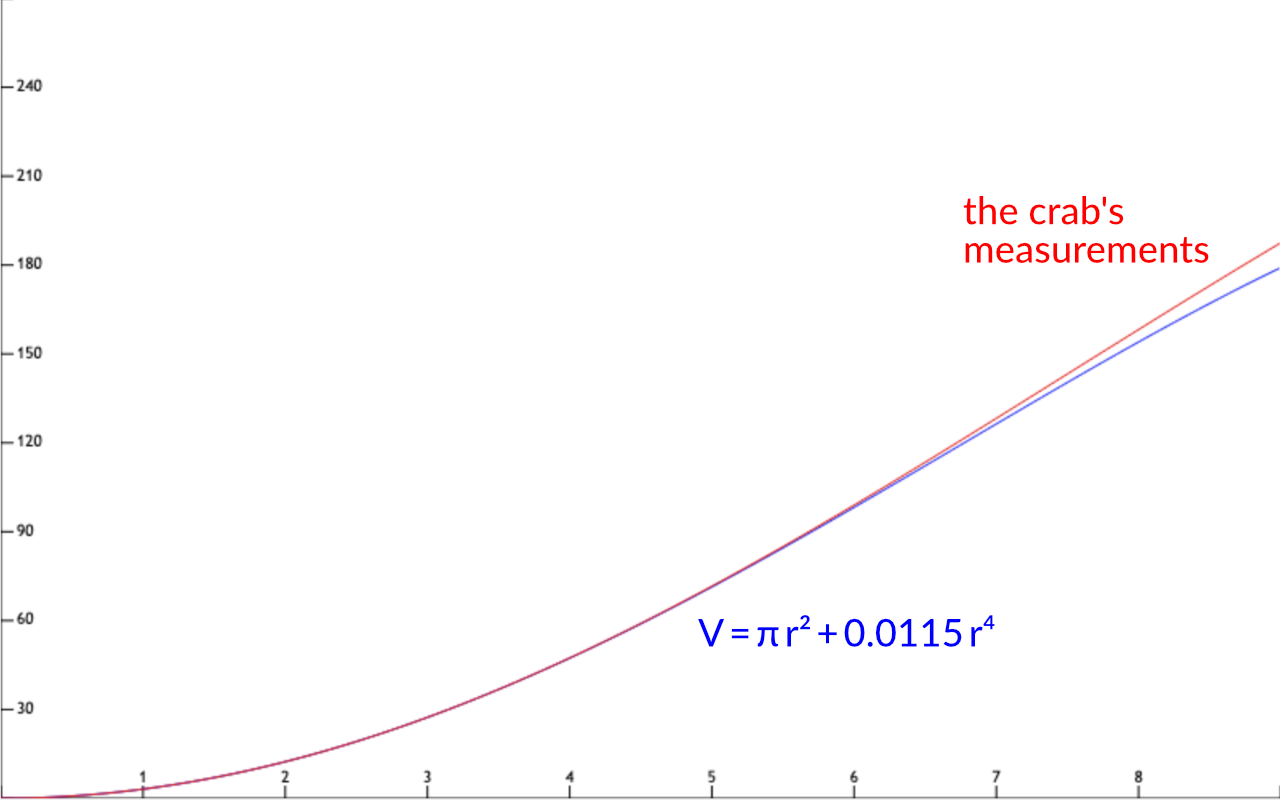
Add one more term – a tiny r6 correction – and the fit is pretty precise:
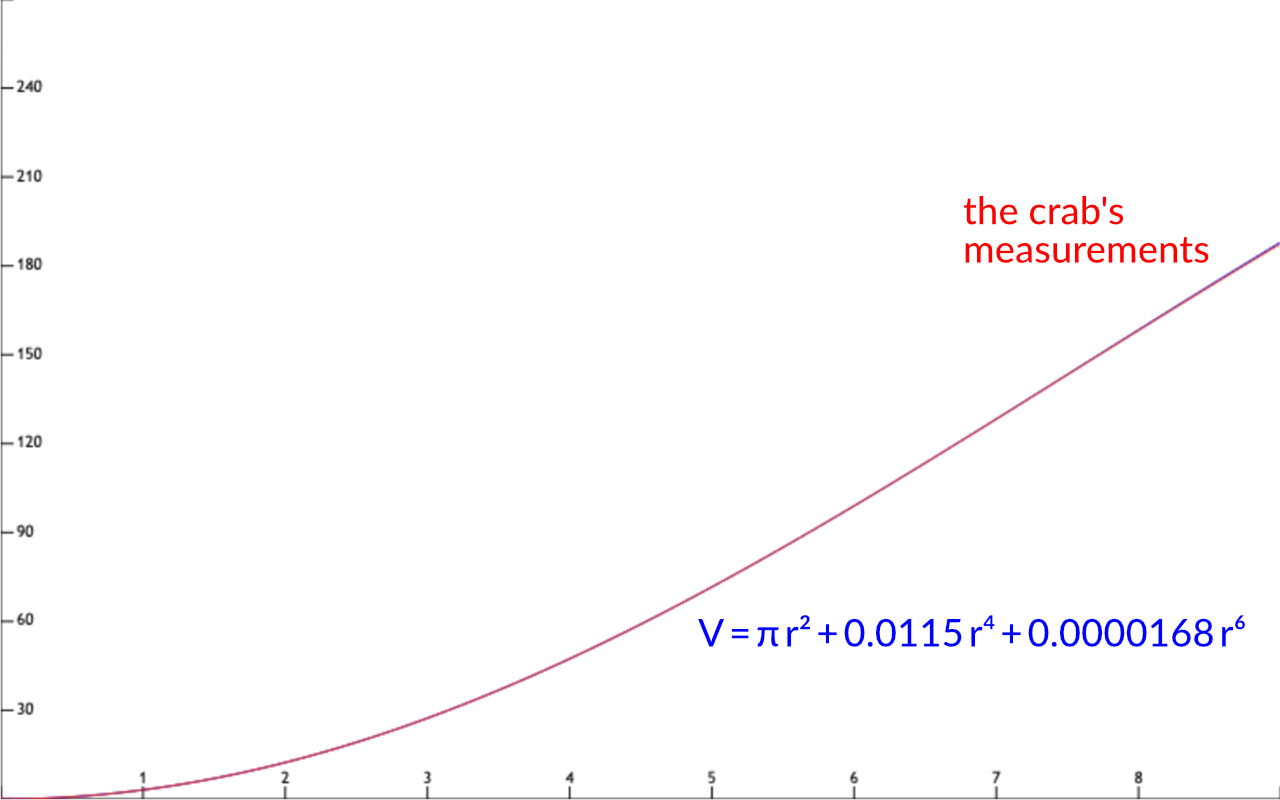
Finally, the crab has its formula for V:
V = π r2 – 0.0115 r4 + 0.0000168 r6
So what’s going on here?
The crab’s universe seems two-dimensional – V = π r2 fits the crab’s measurements reasonably closely – but there’s something else that’s going on that requires a small correction in r4 and a tiny correction in r6.
Suddenly the crab cries: “Eureka!”
That something else that’s going on, it realizes, is curvature.
The crab’s universe is two-dimensional, but it’s curved.
Inside information
To us, with our God’s-eye view of the crab’s two-dimensional space, it’s pretty easy to see what’s going on.
It’s obvious to us that the curvature of the sphere is going to affect how much space the crab covers moving an equal distance in every possible direction.
We can even calculate the formula. For a sphere of radius a, the amount of space the crab covers, V, varies with the distance it moves in every possible direction, r, according to:
V = 2 π a2 (1 – cos r⁄a)
(If you want to know how to derive this formula, take a look at the notes at the end of this article.)
Without going too deeply into the algebra, the cosine in our formula can be expanded into a power series:
cos r⁄a = 1 – (r⁄a)2 / 2! + (r⁄a)4 / 4! – (r⁄a)6 / 6! ...
which gives us:
V = π r2 – π / (12 a2) r4 + π / (360 a4) r6 ...
You might have noticed from my images of the crab’s universe that one crab length equals 2 blue cells on the sphere, and that the circumference of the sphere is 60 blue cells:

This makes the radius of the sphere:
a = 15 / π = 4.77 crab lengths
Plugging this value of a into our formula for V gives us:
V = π r2 – π / (12 × 4.772) r4 + π / (360 × 4.774) r6 ...
And that gives us:
V = π r2 – 0.0115 r4 + 0.0000168 r6 ...
Does that look familiar? It’s the formula the crab arrived at through its polynomial analysis of its measurements.
We can see, from our God’s-eye perspective, that the crab is in a spherical two-dimensional space, with a radius of 15 / π.
But the crab can see it too, from within its universe.
From the 2 in its formula, it knows that its space is two-dimensional:
V = π r2 – 0.0115 r4 + 0.0000168 r6 ...
And it knows that the second term in the formula for a spherical two-dimensional space is:
-π / (12 a2)
where a is the radius of curvature.
So from that second term in its formula:
V = π r2 - 0.0115 r4 + 0.0000168 r6 ...
it knows that:
-π / (12 a2) = -0.0115
Which means that:
a = √(π / (12 × 0.0115)) = 4.77 crab lengths
Ingeniously, our crab has measured not only the dimensionality of its space, 2, but also the radius of curvature of its space, 4.77 crab lengths, from inside its universe.
Higher dimensions
The crab’s method for measuring the curvature of space isn’t limited to two-dimensional space.
It also works in three-dimensional space. Or four-dimensional space. Or space with any other number of dimensions, including fractional dimensions.
Here’s a general formula for how much space the crab would cover moving an equal distance r in every possible direction in d-dimensional space:
V = πd⁄2d⁄2! rd (1 – R6(d + 2) r2 ...)
See Stephen Wolfram’s announcement, under Curvature in Space & Einstein’s Equations, also included as the introduction to his book A project to find the Fundamental Theory of Physics, page 20
In this formula, R is a more general measure of the curvature of a space, called the Ricci scalar curvature.
Once again, what’s the matter?
After all that algebra, let’s remember why curvature matters.
Einstein’s general theory of relativity predicts that matter curves space-time.
If the hypergraph of Wolfram Physics is to be a true representation of the evolution of space over time, then matter must curve the hypergraph too.
To determine whether that’s true, we’re going to need a way to measure the curvature of the hypergraph.
And that’s what our crab has done for us today. It has given us a method for measuring the curvature of space from inside space. It’s a method that’ll work just as well for measuring the curvature of the hypergraph from inside the hypergraph.
The other thing we’re going to need is a way to measure how much matter is there is in a particular region of the hypergraph.
It’s all very well being able to measure the curvature of the hypergraph, but how are we going to know whether the matter in that region of the hypergraph is giving the right amount of curvature if we don’t know how much matter there is?
In my next article, I’ll finally get to that crucial question for Wolfram Physics:
What is matter in the hypergraph?
—
Here’s how I derived the formula for how the amount the crab covers, V, varies with the distance it moves in every possible direction, r, over the surface of a sphere of radius a:
V = 2 π a2 (1 – cos r⁄a)
Imagine the crab has already moved a distance r from its starting point in every possible direction, covering a curved circle of radius r on the surface of the sphere.
Looking a cross-section of the sphere above, you can see that the angle at the centre of the sphere between the crab’s starting point at the top and the point it reaches moving a distance r in any direction is r⁄a
Why? Because arc length = radius × angle in radians.
So the radius of the circle in three-dimensional space is a sin r⁄a
Why? Because in that right-angled triangle on the cross-section, the angle is r⁄a, the opposite edge is the radius of the circle and the hypotenuse is the radius of the sphere, and sin angle = opposite / hypotenuse.
Now imagine the crab moves a short distance dr further in every possible direction, covering an additional curved ring on the surface of the sphere, with radius r and width dr.
The additional space it has covered is the area of the curved ring, which is, near enough, its circumference, 2 π times the radius of the circle we calculated above, a sin r⁄a, times the ring’s width, dr. That’s 2 π a sin r⁄a dr.
Why? Because the circumference of a circle is 2 π × radius. Why is near enough good enough? Because we’re going to shrink dr to zero, and in that limit, these formulae are exact.
The area of the curved circle covered by the crab, V, is simply the sum of the areas of all the curved rings it covers as it goes a short distance dr further from 0 to r. We can use integration to sum these areas:
V = ∫ 0r 2 π a sin r⁄a dr
Why? Because an integral is the continuous analog of a sum, which is used to calculate areas, volumes, etc.
∴V = – 2 π a2 [ cos r⁄a ] 0r
Why? Because ∫ sin kx dx = – 1⁄k cos kx + C.
∴V = 2 π a2 (1 – cos r⁄a) QED