In his General Theory of Relativity, Einstein combined the three dimensions of space with the one dimension of time in what we now know as Einstein’s equations.
Ever since, physicists have thought of space and time as effectively the same thing: components of four-dimensional space-time.
This might be the biggest blunder physicists have ever made.
Stephen Wolfram, on page 22 of his book A project to find the Fundamental Theory of Physics, calls it the “one ‘wrong turn’ in the history of physics in the past century”.
Space-time is dead.
Here’s why... and how physicists got it so wrong for so long.
How space-time was born
Einstein’s equations may be written as:
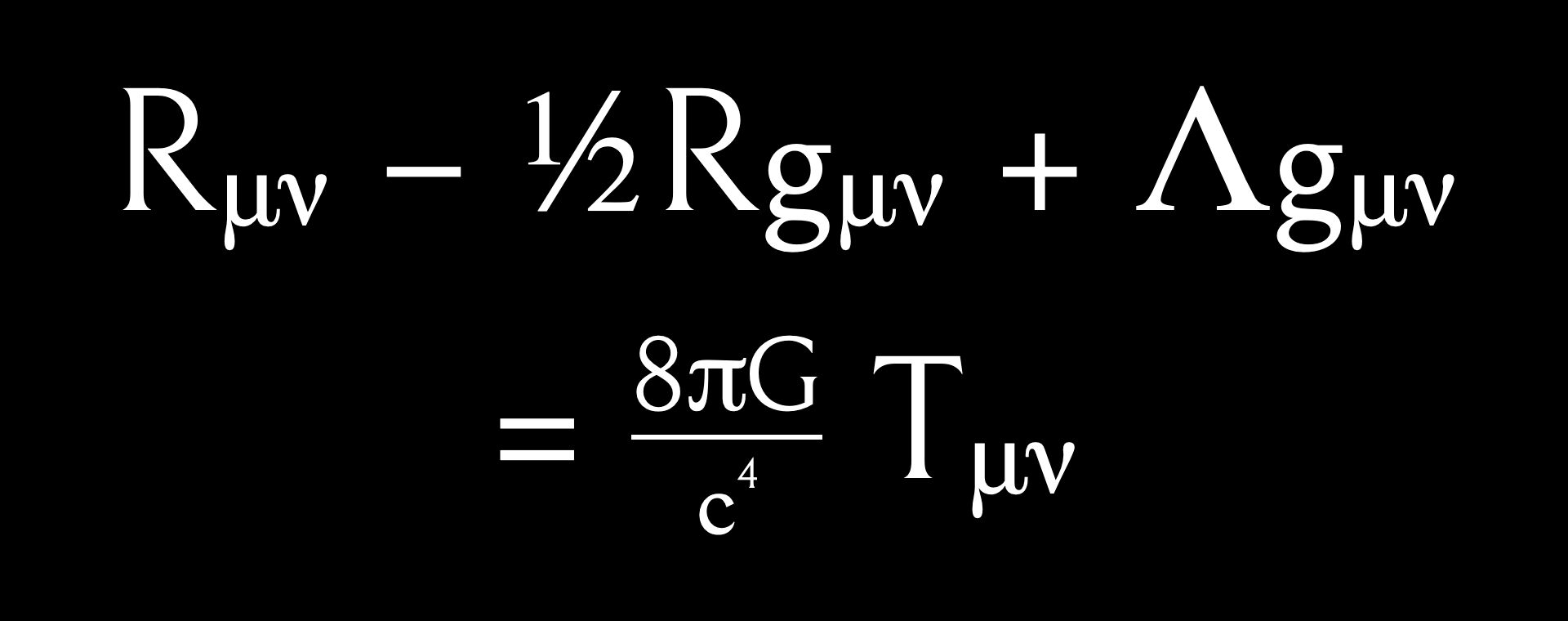
Not quite as snappy as E = mc2, but still.
This equation describes how space and time are distorted by matter.
In other words, it explains gravity.
The elements of the equation are tensors.
You’ll be relieved to hear that I’m not going go into what a tensor is.
The only thing you need to know is that the tensors in Einstein’s equations don’t distinguish between the three dimensions of space and the one dimension of time.
As far as the equations are concerned, it’s all the same.
Space? Time? Who cares? Einstein’s equations make no distinction. That’s part of their beauty.
It was natural for physicists to refer to the four-dimensional structure represented in the tensors as space-time.
It’s a beautiful concept. It allowed for succinct explanations. How to describe the orbit of the Earth around the Sun? Well, the matter in the Sun distorts space-time as predicted by Einstein’s equations, and the Earth follows the shortest possible path through that distorted manifold.
Space-time. It’s an abstract concept. It’s a mathematical construct. It’s an explanatory tool. No problem.
Except that the physicists didn’t stop there.
Once space-time has worked its way into their heads, they couldn’t help but think of it as real.
Space? Time? So last century. In reality, they’re just components of four-dimensional space-time.
Nor did the physicists didn’t stop there.
If space and time are just components of four-dimensional space-time, they insisted, really space and time are the same thing.
Space? Time? No difference.
This, of course, is insane.
Space ≠ time
Space and time are not the same thing.
Obviously.
Here’s a quick demonstration.
First, I’m going to stop this stone’s movement through space.
There, I did it! The stone is motionless in space, more or less.
I know, I know, in reality, the stone’s spinning around the Earth’s axis at high speed, and both the stone and the Earth are orbiting the Sun at high speed, and the stone, the Earth and the Sun are orbiting the galaxy at high speed, and the stone, the Earth, the Sun and the galaxy are... well, you get the picture.
But you can’t spoil my demonstration my switching reference frames on me. In the reference frame of this room, I just stopped the stone. Give me any other reference frame, and the appropriate rocketery, and I could stop the stone in that reference frame too.
Next, I’m going to stop the stone’s movement through time.
Oops, that didn’t work, the stone’s still moving through time.
Let me try again.
OK, that still didn’t work. No matter what I do, the stone continues to move through time.
Why is it possible to stop a stone’s movement through space, but impossible to stop its movement through time?
Well, because space and time are fundamentally different things.
Obviously.
How time lost its arrow
Here’s another thing about the tensors in Einstein’s equations. They don’t distinguish between the three dimensions of space and the one dimension of time; that’s one thing. But they also don’t distinguish between a backward and a forward direction of time.
This was also true of earlier theories of physics. Newton’s laws of motion didn’t distinguish between a backward and a forward direction of time, either.
You can probably guess the leap the physicists made from here.
If time is just another component of four-dimensional space-time, they insisted, with no arrow to distinguish between backward and forward directions, then really time doesn’t have an arrow.
Past? Future? No difference.
This, too, is insane.
Past ≠ future
Time does have an arrow.
Obviously.
Here’s a quick demonstration.
First, I’m going to move this stone backwards and forwards through space.
Backwards. Forwards. Backwards. Forwards. Easy!
Next, I’m going to move the stone backwards and forwards through time.
Forwards. Forwards. Forwards. This is hard.
Wait, let me try again.
Forwards. Forwards. Forwards.
I guess it’s not so easy to move a stone backwards in time.
Hang on, let me go get my time machine...
Actually, on second thoughts, I’ll save the time machine for a future article.
Why is it possible to move a stone forwards through time, but impossible to move it backwards through time?
Well, because time has an arrow.
Obviously.
Why deny the obvious?
It’s fun to witness physicists’ efforts to wriggle out of the consequences of their pretence that time is the same as space.
One of my favourites is Stephen Hawking’s contention that the arrow of time can be rescued through a slightly desperate reversal of the Second Law of Thermodynamics.
That’s the one that states that entropy increases over time. In other words, the more time passes, the messier the universe gets.
Hawking reversed this, stating that the arrow of time is the direction in which entropy increases. In other words, if you’re wondering whether you’re going forwards or backwards through time, just take a quick Marie Kondo look at the universe: if it’s getting messier, you’re going forwards through time; if it’s getting tidier, then you’re in a time machine going backwards through time.
I don’t want to make too much fun of this argument. It’s actually rather brilliant. But there’s no denying that it’s also slightly desperate.
Why do physicists feel they have to resort to such academic acrobatics to explain the arrow of time?
The reality of equations
Here’s the thing: when physicists come up with equations as exquisite as Einstein’s, they stop thinking of them as a model of reality and start thinking of them as reality.
They’ve always done this.
Remember the crystalline spheres I talked about in Beware invisible things? The Ancient Greeks came up with equations that described the motion of the planets as circular trajectories around the Earth. This worked so well that they stopped thinking of these equations as a model of reality and started thinking of them as reality: they imagined real crystalline spheres that carried the planets around the Earth.
Enlightenment physicists weren’t so easily fooled. Newton came up with much better equations that described the motion of the planets as an acceleration towards the Sun that varied with their masses and the inverse square of the distance between them. This worked so well that physicists stopped thinking of Newton’s equations as a model of reality and started thinking of them as reality: they imagined real gravitational forces between the Sun and the planets to explain their acceleration.
Twentieth century physicists weren’t so easily fooled. As we’ve seen, Einstein came up with even better equations that described the motion of the planets as the shortest possible path through four-dimensional space-time, as distorted by the Sun. This worked so well that physicists stopped thinking of Einstein’s equations as a model of reality and started thinking of them as reality: they imagined that space-time is real; they jumped to the conclusion that space and time must therefore be the same thing; they indulged in academic acrobatics to explain how time can seem different from space even though the equations made no distinction between them.
Ascribing reality to equations can be a powerful tool in physics.
For example, when our equations for black body radiation and the photoelectric effect indicated that light is emitted and absorbed in quanta, physicists were reluctant to conclude that light is actually quantized... until a brilliant young physicist named Albert Einstein ascribed reality to those equations and thereby discovered the photon.
But like all powerful tools, ascribing reality to equations can be dangerous.
Time and time again through the history of physics, we’ve slipped from thinking of our equations as a model of reality into thinking of them as reality... only to discover that reality is as elusive as ever.
Space and time in Wolfram Physics
In Wolfram Physics, space and time are unequivocally different things.
Space is the graph.
Time is the evolution of the graph.
Take this graph, for example:
The separation of the nodes by the edges represents the separation of different locations in space. The graph is space.
Now let’s apply a rule to the graph:
The evolution of the nodes and edges of the graph represents the evolution of the universe over time. The evolution of the graph is time.
By these definitions, space and time are definitely not the same thing.
They’re fundamentally different things.
Obviously.
Time does have an arrow.
When we apply a rule to the graph, time moves forwards.
Time doesn’t move backwards.
Obviously.
There’s no such thing as space-time in Wolfram Physics. General Relativity emerges from the evolution of the graph. It’s a wonderful symmetry that there’s no distinction between space and time in the ensuing equations. But it’s no more than that: a wonderful symmetry.
Physicists took a wrong turn when they stopped thinking of Einstein’s equations as a model of reality and started thinking of them as reality.
Space-time is dead.
Mercifully.
The model of space and time that takes its place in Wolfram Physics makes a whole lot more sense to me than space-time ever did.