What if you’re inside a universe and you want to know whether space is curved?
Well, there’s a way to find out that’s so simple that even a crab or a space frog could do it.
Here’s how to tell if your universe is curved.
—
I’ve already talked about how to tell whether your universe is two-dimensional, or three-dimensional, or has some other number of dimensions.
Remember I asked you to imagine a two-dimensional crab in a two-dimensional universe:
By moving an equal distance in every possible direction, and measuring how much space it covers:
the crab can calculate the dimensionality of its universe, from inside that universe.
I applied this method to measure the dimensionality of the hypergraphs of Wolfram Physics:
But I made an assumption in these calculations of dimensionality.
I assumed that space is flat.
I pictured the crab moving across a flat, two-dimensional space.
Or a flat, three-dimensional space.
But what if space isn’t flat?
What if the universe is curved?
Warped worlds
This might seem like an odd question to ask.
Why would space be curved?
What would that even look like?
I mean, it’s possible to imagine a two-dimensional universe being curved. If you think of a two-dimensional crab moving across a two-dimensional sheet of paper, you can imagine that sheet of paper being flat, like this:

or curved, like this:

But it’s more difficult to imagine a three-dimensional universe being curved. Try it. Try to imagine a curved three-dimensional space. Can you make an image of it in your mind? I know I can’t.
So why am I asking such an odd question?
Well, it’s important to ask whether the universe is curved because it turns out that our universe is curved.
According to Einstein’s general theory of relativity, three-dimensional space is curved.
Or, to be more precise, four-dimensional space-time is curved.
(I know what you’re thinking: isn’t space-time dead? But let’s not get into that again.)
To be even more precise, our four-dimensional space-time is curved by the presence of matter.
If Wolfram Physics is to be a true model of our universe, then the space represented by the hypergraph must also be curved by the presence of matter.
So, if we want to know whether the Wolfram model holds water, we’re going to need some way to determine whether a hypergraph is curved.
Parallel lines never meet
Euclid postulated that parallel lines never meet.
And that’s true... if space is flat.
Let me tell you a story about parallel lines.
Once upon a time, a couple of two-dimensional crabs lived a short distance from each other in a flat two-dimensional space:
One day, they started moving in the same direction:
As they continued in that direction, they noticed something strange. No matter how far they moved, they remained at the same short distance from each other:
And their paths remained parallel ever after:
And that’s how the crabs knew that their space was flat.
Parallel lines do meet
Flat spaces make for dull fairy tales.
Let me tell you another story about parallel lines, this one set in a curved space.
Once upon a time, a couple of two-dimensional crabs lived a short distance from each other in a spherical two-dimensional space:

It’s a bit like the crabs’ living a short distance from each other on the equator of the Earth, say, at São Tomé and Kampala:
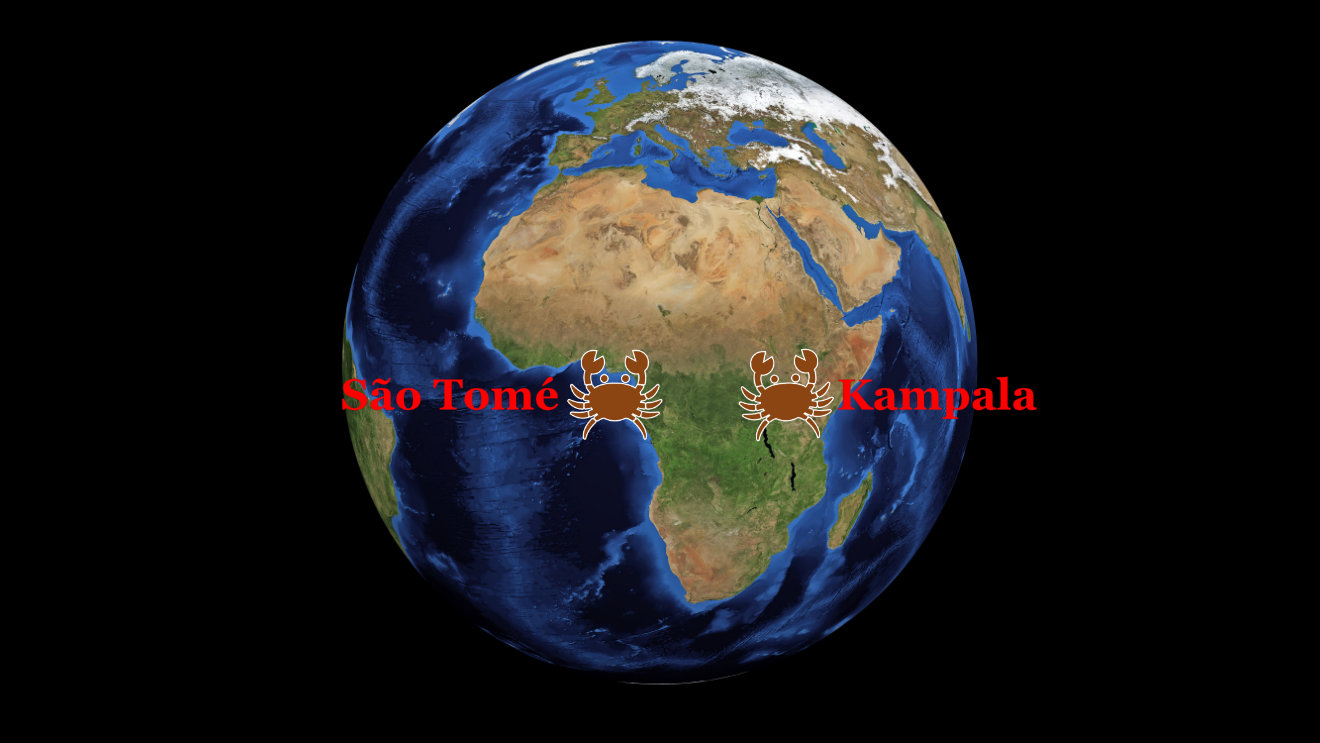
You just have to remember that unlike us three-dimensional humans, who can leave the surface of the Earth in rockets and see that it’s curved, the two-dimensional crabs are forever confined to their spherical two-dimensional space: they can’t leave it; they can’t see that it’s curved.
One day, the crabs started moving in the same direction:

It’s the same as if the crabs were both moving north on the surface of the Earth:
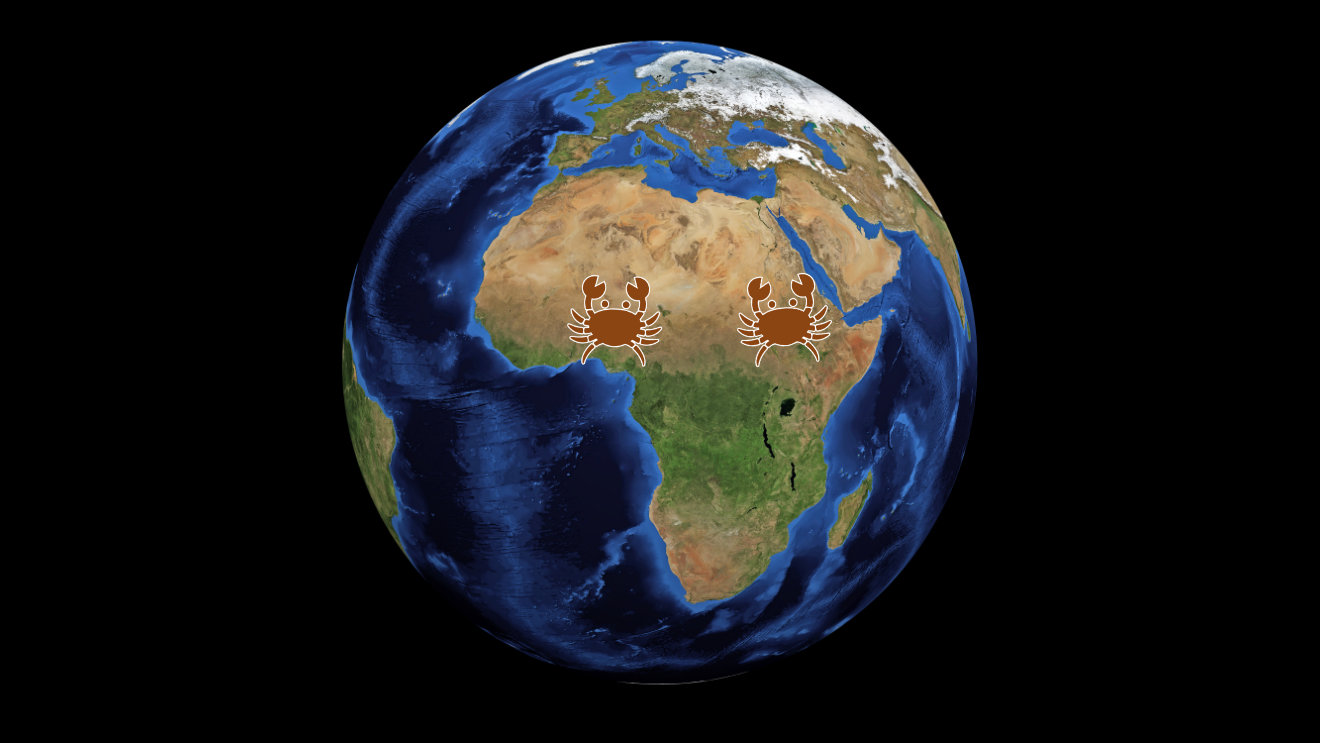
At first, the crabs seemed to remain the same distance apart:

After all, they were moving in the same direction, north, so they were moving along parallel paths:
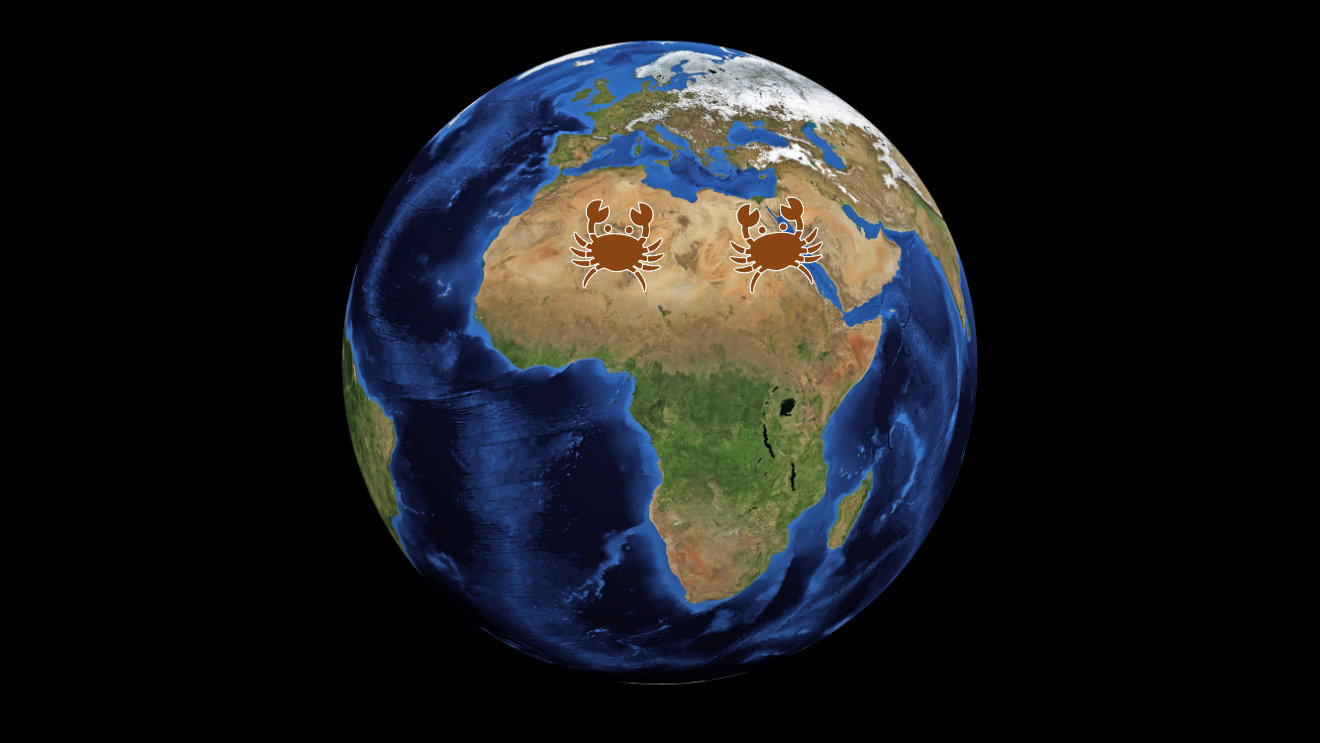
After a while, however, they noticed something strange. They seemed to be getting closer together:

One of the crabs shouted to the other: “You’re veering off-course!”
The other crab shouted back: “No, I’m not, I’m moving in a straight line, not an inch to the left, not an inch to the right, dead ahead. You must be veering off-course!”
Of course, neither of them had been veering off-course, both of them had been moving in a straight line.
It’s as if the crab that had started in São Tomé had followed a true north course to Biskra, and the crab that had started in Kampala had followed a true north course to Paphos:
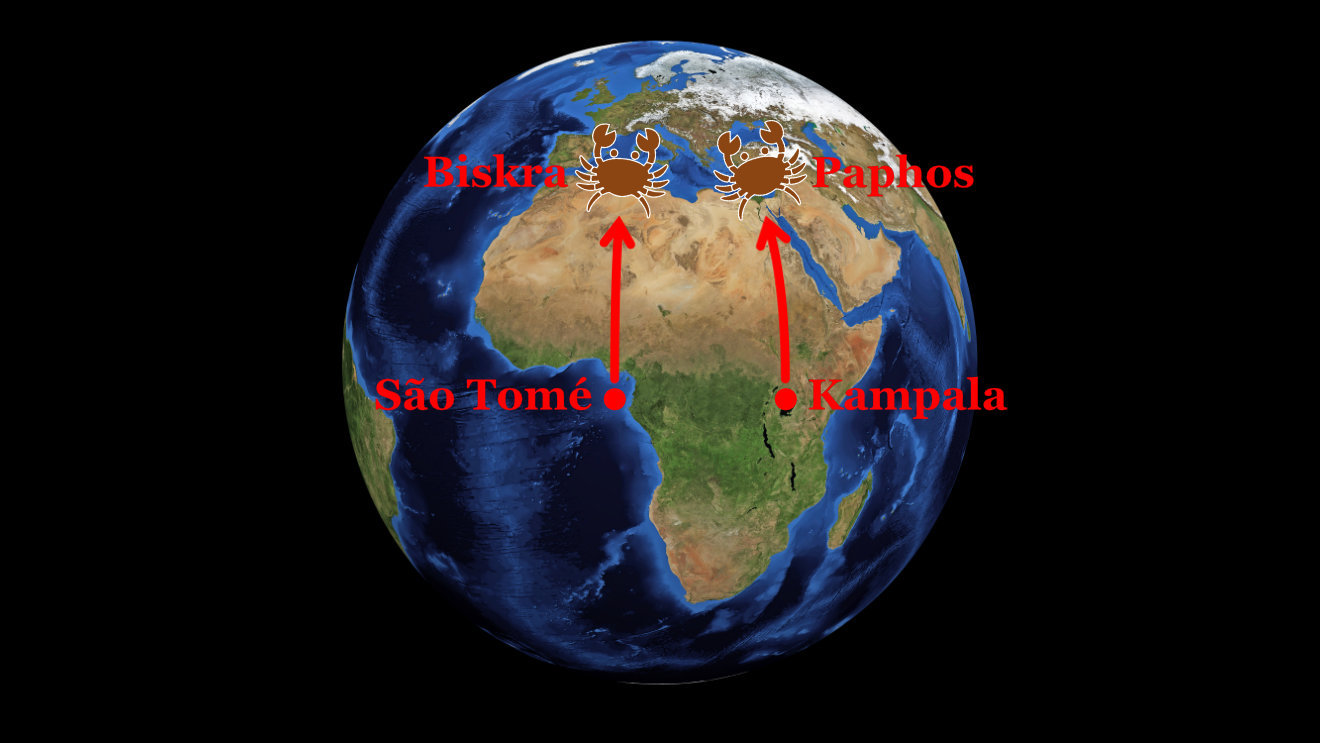
When they’d started out at the equator, at São Tomé and Kampala, they’d been nearly 1,800 miles apart, but now that they were further north, at Biskra and Paphos, they were a mere 1,500 miles apart.
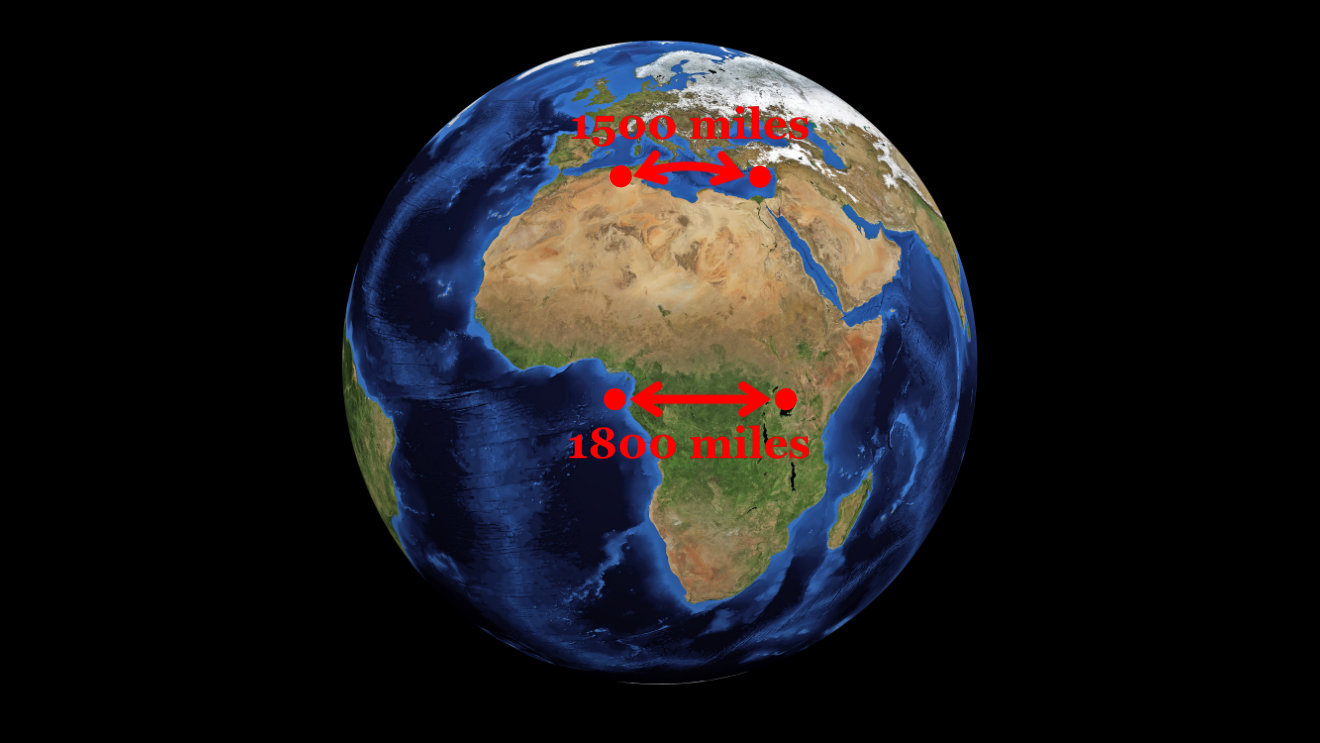
Why? If the Earth were flat, the two crabs, moving in the same direction, due north, would have remained the same distance apart. But the Earth isn’t flat. It’s round. Its surface is curved.
As the two crabs continued along their parallel paths, something even stranger happened. They met:

It’s the same as if, moving north from their separate starting points on the equator, they’d met at the north pole:
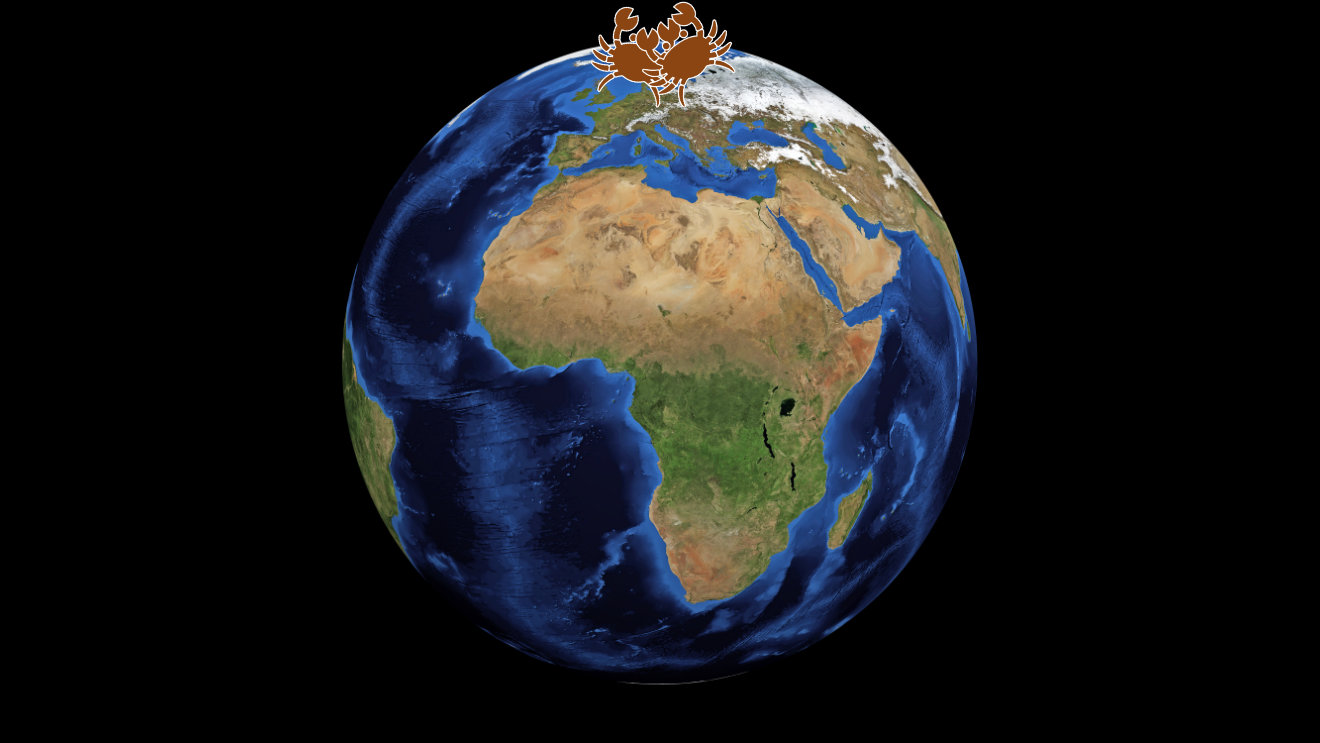
Euclid was wrong. If a two-dimensional space is not flat, then parallel lines do meet.
And that’s how the crabs knew that their space was curved.
Frogs in space
Now let’s see how this works in a three-dimensional universe, like our own.
A long time ago, in a galaxy far, far away, a couple of three-dimensional frogs floated a short distance from each other in a flat three-dimensional space:

One day, they started moving in the same direction:
As they continued in that direction, they noticed something strange. No matter how far they moved, they remained at the same short distance from each other:
And their paths remained parallel ever after:
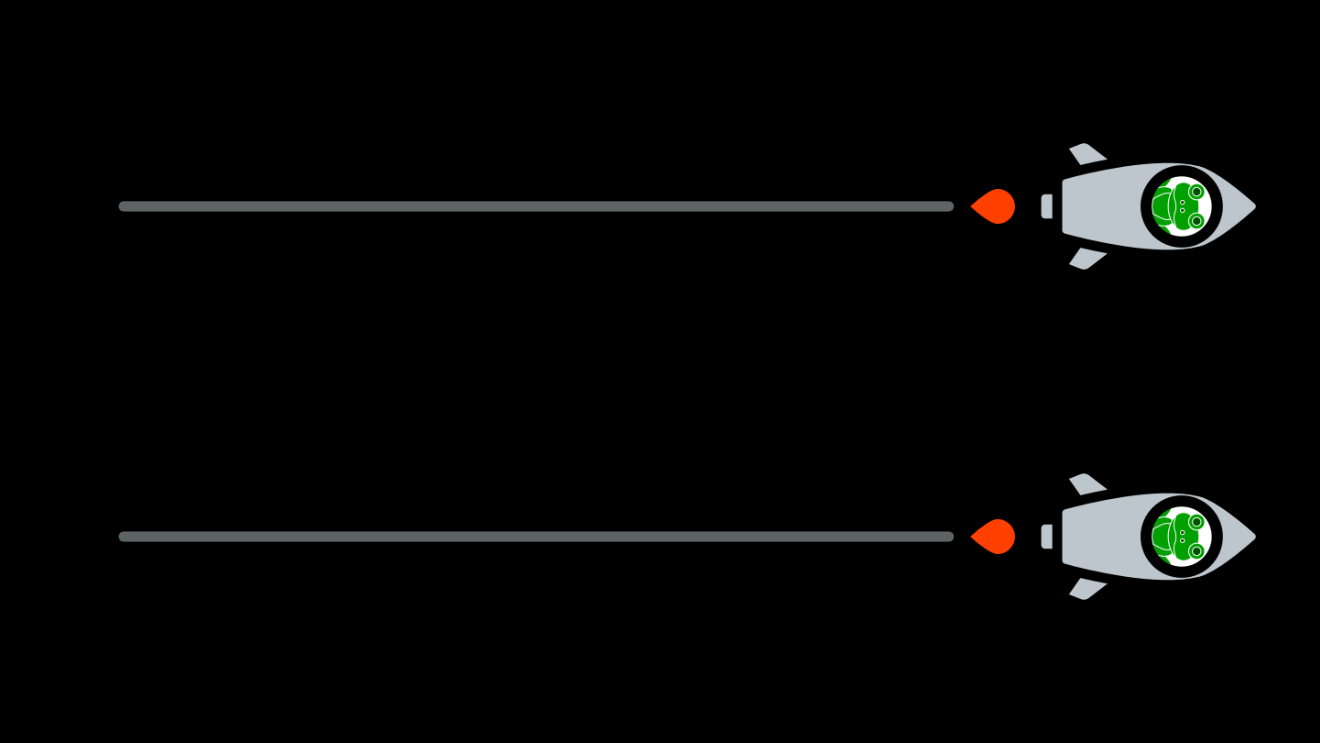
And that’s how the frogs knew that their space was flat.
Ground control to Major Frog
Flat spaces make for dull space operas, too.
So let’s bring this home.
A long time ago, in a galaxy not so far away, a couple of three-dimensional frogs floated a short distance from each other, quite close to a planet called Earth:

One day, the frogs started moving in the same direction:

At first, they seemed to remain the same distance apart:
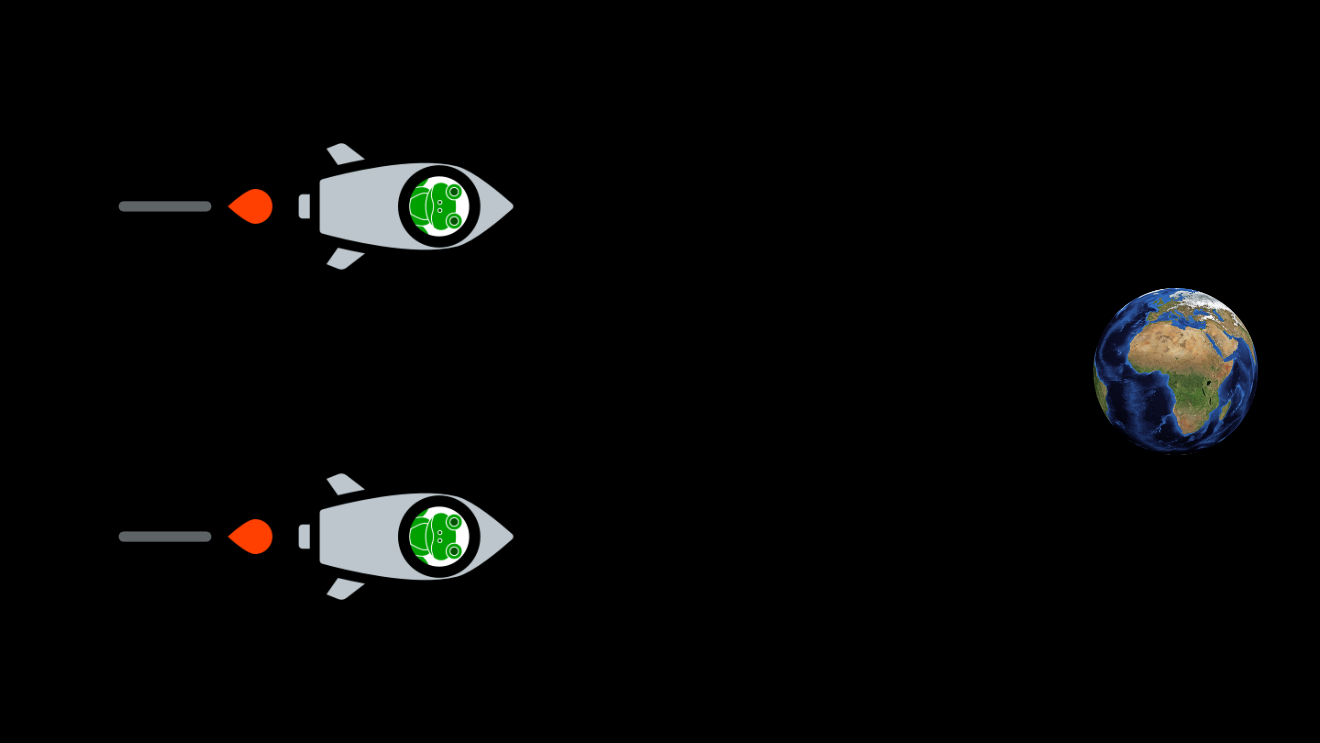
After a while, however, they noticed something strange. They seemed to be getting closer together:
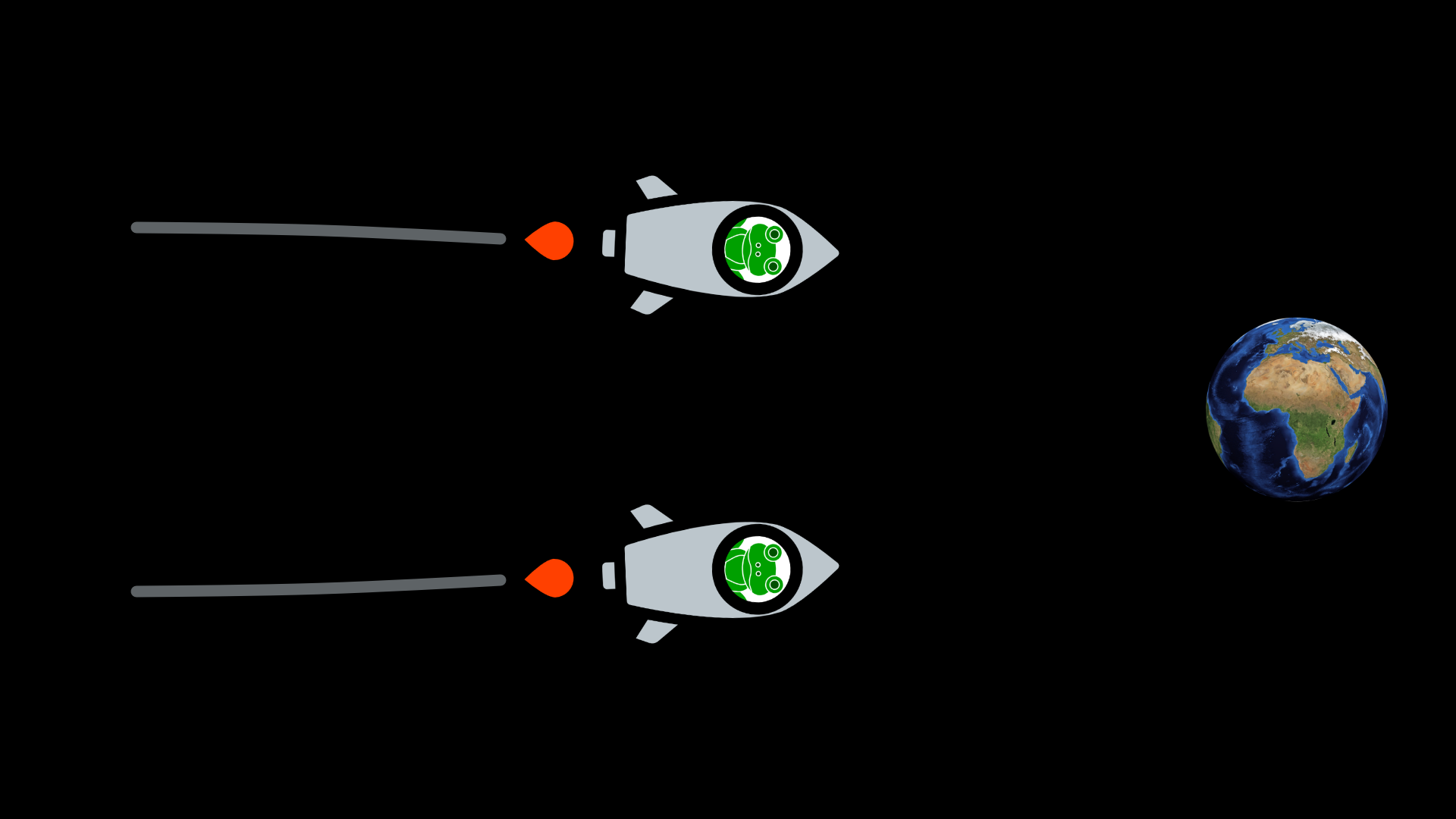
One of the frogs shouted to the other: “You’re veering off-course!”
The other frog shouted back: “No, I’m not, I’m moving in a straight line, not an inch to the left, not an inch to the right, dead ahead. You must be veering off-course!”
As the two frogs continued along their parallel paths, they got closer and closer:
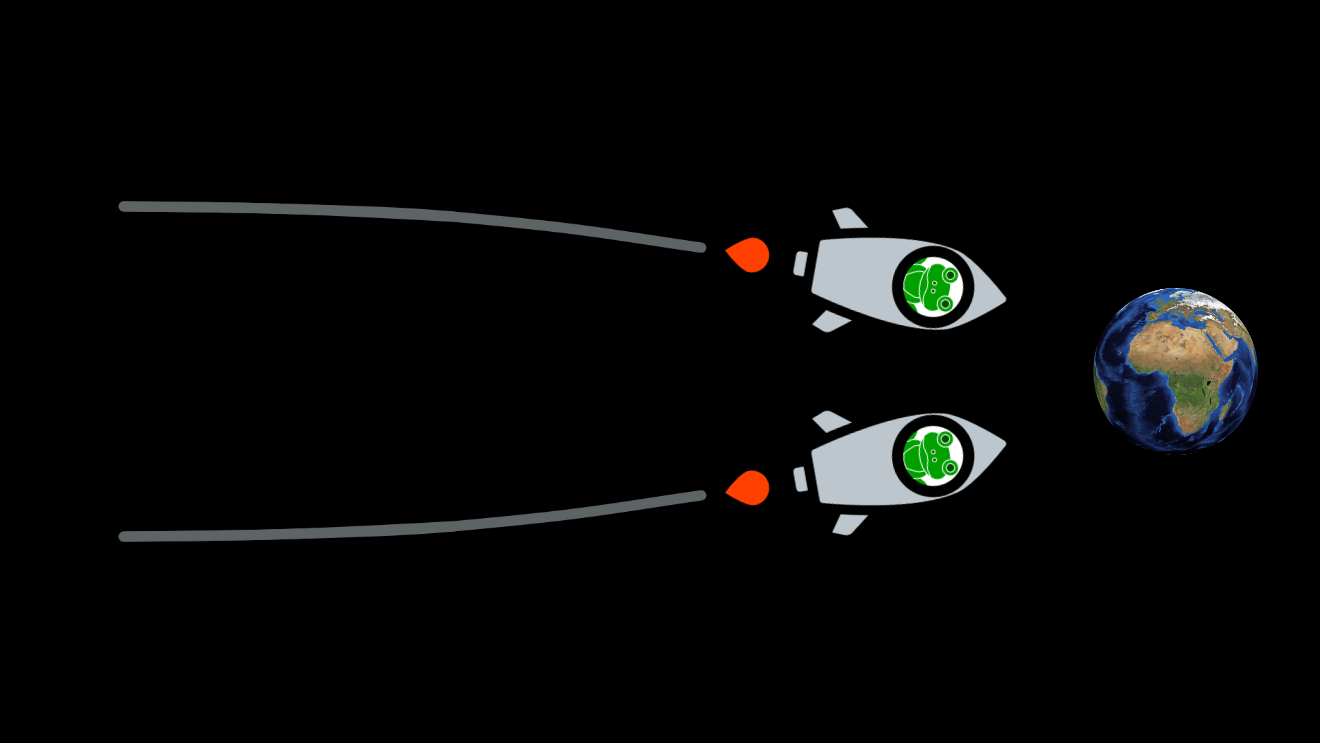
One of the frogs, whose name was Newton, came up with an explanation for the convergence of their parallel paths. “There must be an invisible force,” he said, “that’s pulling us both towards the Earth. Let’s call it gravity!”
The other frog, whose name was Einstein, came up with a different explanation. “I’ve seen this before,” he said. “If space is flat, then Euclid was right: parallel paths don’t converge. But if space is curved, then Euclid’s wrong: parallel lines can meet.”
Finally, the two frogs touched down on Earth, and met at a tea shop in São Tomé:
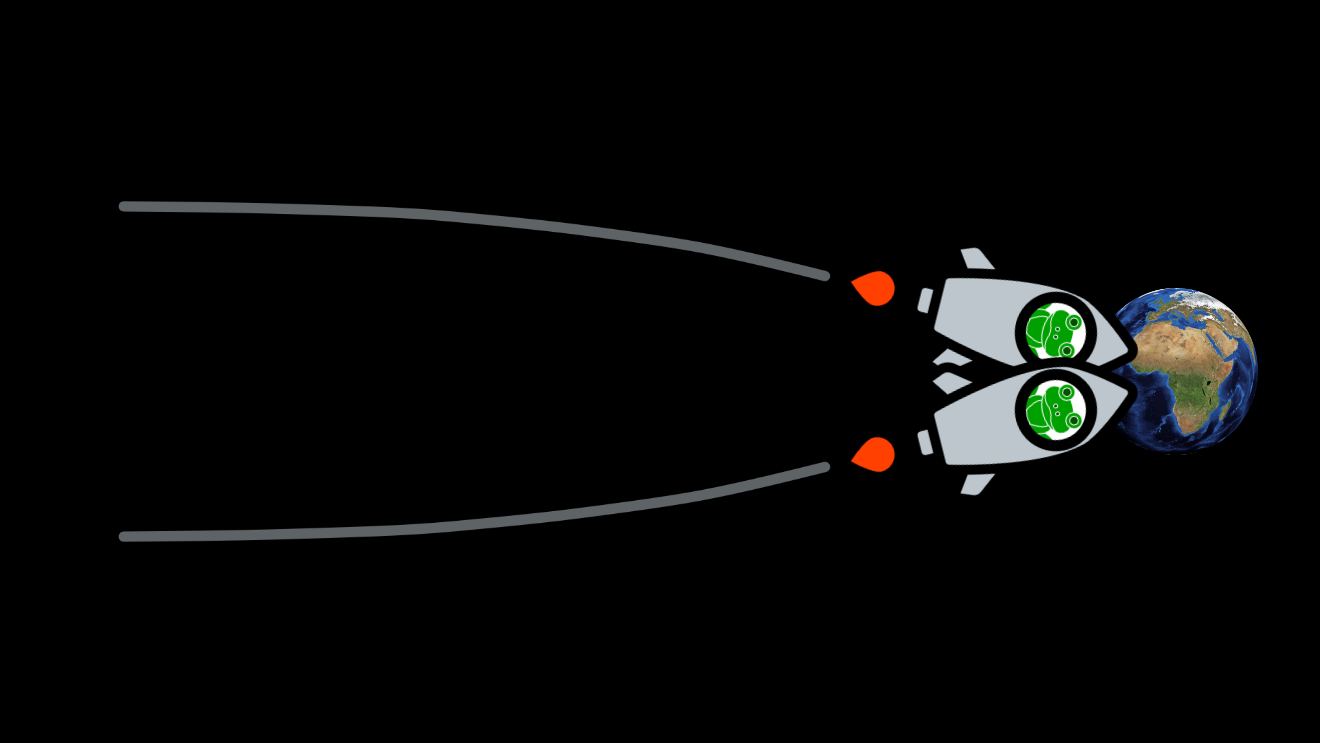
And that’s how the frogs knew that their space was curved.
What’s the matter?
Einstein’s explanation of why we fall towards the Earth was brilliant. He didn’t need to postulate some invisible gravitational force. He just took our motion towards massive bodies like the Earth as evidence that matter curves space.
Nor did Einstein need to postulate some invisible fourth dimension in which three-dimensional space is curved. We’re three-dimensional creatures. We can’t jump out of our three-dimensional universe, take a look at it from the outside, and say, hang on a minute, our space is curved! Fortunately, we don’t need to. We can determine that our space is curved from inside our universe. Our motion towards massive bodies like the Earth gives the game away.
This is the crux of Jonathan Gorard’s derivation of Einstein’s equations from the Wolfram model.
To derive General Relativity from Wolfram Physics, we’re going to need to determine that the hypergraph is curved, in the same way that the crabs and frogs in this article determined that their space is curved.
And we’re going to need to measure the curvature of the hypergraph. In my next article, I’ll show you how crabs and frogs can measure how curved their space is, from inside their universe.
And we’re going to need to show that the curvature of the hypergraph is related to the presence of matter in precisely the way that Einstein predicted.
And to do that, we’re going to need to tackle another question:
What is matter in the hypergraph?