I’ve talked about the basic concepts of Wolfram Physics: nodes, edges, graphs & rules.
I just threw these concepts out there. No explanation. No rhyme, no reason. Nodes, edges, graphs & rules. Take them or leave them.
Naturally, this raised a few questions in some people’s minds.
These questions can be summed up as follows:
Wait... What? Nodes, edges, graphs & rules? Why?
This a deep question.
Let’s get into it.
What do we see in the universe?
At the end of my article Different rules, different universes, I asked the question: What does our universe look like?
If we’re going to satisfy ourselves that the nodes, edges, graphs & rules of Wolfram Physics are a true representation of our universe, we need to be clear on what our universe looks like.
When we look at the universe, what do we see?
Well, here are a few things.
We see space. We see time. We see matter.
Think of that stone I held in my hand last time. It’s made of something: matter. When I dropped it, it fell through space. A short time after I dropped it, I caught it in my other hand.
Space. Time. Matter.
We could go into a lot more detail on each of these, but just recognizing that these are things we observe in our universe is a start.
If our nodes, edges, graphs & rules don’t look like space, time and matter as we observe them in our universe, then they’re not going to work as a theory of physics.
What about the higher things?
Space, time and matter aren’t the only things we see in the universe.
We see life. We see consciousness. We see meaning.
These things are more important to us than space, time and matter. Who cares about falling stones? What we really care about are the higher things.
Life. Consciousness. Meaning.
Here’s the bad news: these things may be beyond the scope of any theory of physics, let alone theories as fundamental as Stephen Wolfram’s.
But here’s the good news: I’m not going to cop out entirely on the questions of life, consciousness and meaning. They’re too fascinating for me to retreat into narrow reductionism. I’ll return to them in future articles.
What are the characteristics of space?
In this article, however, I’m going to focus on the first of those three fundamental things we see in our universe: space.
What is space?
What does it look like?
We’re taught in school that space is three-dimensional.
Imagine for a moment that you hadn’t been taught that space is three-dimensional. How would you think about space?
Here’s how the Polynesians, who navigated their way by canoe between hundreds of Pacific islands, once represented their world:

These days, our maps are so precise, with every location plotted at exact latitudes and longitudes, that we forget how the world once appeared to us.
The Polynesians represented Pacific islands as points, and the ocean currents between those islands as lines between those points.
You might notice a passing resemblance between these stick charts and the nodes and edges of Wolfram Physics we’ve been exploring in the last few articles:
The nodes look a little like the shells representing islands on the stick charts, and the edges look a little like the sticks representing the routes between them.
Let me be clear: the graphs of Wolfram Physics are on an entirely different scale from these stick charts.
The routes between the islands on the charts represent distances of maybe a hundred miles, around 105 metres.
The edges between the nodes on our graphs respresent distances of, who knows, maybe 10-100 metres.
105 metres versus 10-100 metres: that’s an unimaginable difference in scale.
Still, it’s promising that some of the graphs of Wolfram Physics show some of the same characteristics of space that we see in these beautiful stick charts.
Let’s dig a little deeper into what these characteristics of space are.
Characteristic 1: Position
In our universe, things have positions in space.
Take any one of the shells on the stick chart:

It’s not just anywhere.
It’s somewhere.
It’s right here, at this position in space, rather than any other position in space.
Same goes for the island it represents.
That island isn’t just anywhere in the Pacific.
It’s somewhere in the Pacific.
And that’s true of the nodes on our graphs, too.
Take any one of those nodes:

It’s not just anywhere on the graph.
It’s somewhere on the graph.
So far, so good.
Characteristic 2: Distance
In our universe, some things are further apart than others.
Take two shells that are close together on the stick chart:

They’re separated only by a short length of stick on the chart. The islands they represent are a relatively short canoe ride apart in the Pacific.
However, take the shell on the far left of the chart and the one on the far right of the chart:

These two shells are a long way apart. To get from one to the other on the chart, you have to traverse many different sticks. To paddle between the islands they represent in the Pacific, you have to ride many different currents, no doubt stopping at some of the islands along the way.
And again, that’s true of the nodes on our graphs, too.
Take two nodes that are connected by a single edge:
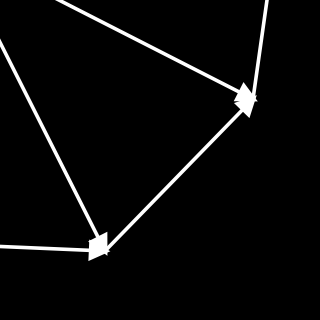
When I wrote the software to render the graph, I designed it to show these two nodes close together, because you only have to traverse that one edge to get from one to the other.
However, take the node on the far left of the graph and the one on the far right of the graph:

To get from the far-left node to the far-right node on the graph, you have to traverse many different edges. So I designed the software to show these two nodes far apart.
Note that it’s not the lengths of the edges that matter here. Those lengths are arbitrary: I designed the software to make all the edges as close as possible to the same length.
What matters is the number of edges you need to traverse to get from one node to another.
That concept of the number of edges of two nodes on the graph looks like a pretty good representation of our concept of the distance between two points in space.
Again, so far, so good.
Looks familiar
Position and distance aren’t the only characteristics of space we’ll want to reproduce in Wolfram Physics.
And space isn’t the only thing we see in the universe that we’ll also want to see in our nodes, edges, graphs & rules.
There’s time, too, remember.
And matter.
Not to mention myriad other aspects of our universe.
Still, position and distance are a start.
We can look at some of the graphs of Wolfram Physics and immediately recognize at least these two fundamental characteristics of space in what we see.
Some of our graphs, at least, look a little like space as we know it, space as the Polynesians once represented it in their stick charts:
Why nodes, edges, graphs & rules?
Because they look a little like our universe.
Of course, the nodes, edges, graphs & rules of Wolfram Physics are going to have to look a lot like our universe if it’s to be a viable theory of physics.
We’ll get there.
Next time, I’ll go beyond position and distance, and introduce a few other characteristics of space we’ll want to reproduce in Wolfram Physics.
The more of these characteristics we introduce, the better we’ll be able to distinguish between rules that yield unfamiliar universes, and rules that yield universes that look a little like our own.
—
Micronesian navigational chart (adapted) by Cullen328 reproduced under CC BY-SA 3.0